SISTEMA NUMÉRICO
Números Reales
Los números que se
utilizan en las matemáticas son los números reales. Hay
un número real en cada
punto de la recta numérica. Los números reales se
dividen en números
racionales, números irracionales y números enteros los
cuales a su vez se
dividen en números negativos, números positivos y cero (0)
Podemos verlo en esta
Gráfica:
Un número real es racional si se puede
representar como cociente a/b, donde a
sea un entero y b sea un entero no igual a cero.
Los números racionales pueden
escribirse en forma decimal. Existen dos maneras:
* Decimales terminales
* Decimales que se repiten infinitamente
Programa de Tecnología Componente Científico
Semana de Inducción
Los números reales que no pueden ser expresados
en la forma , donde a y b
son enteros se llaman números irracionales. Los
números irracionales no tienen
decimales terminales ni decimales que se repiten infinitamente.
1.2 Reglas Importantes para Resolver
Operaciones Aritméticas:
¸ Primero resolver todo lo que esté dentro de
símbolos de agrupación.
¸ Evaluar las expresiones exponenciales.
¸ Hacer todas las multiplicaciones y divisiones
en orden de izquierda a derecha.
¸ Hacer todas las sumas y restas en orden de
izquierda a derecha.
Operaciones básicas de la suma o “adición”
- En una adición los términos que se suman se
denominan sumandos y el
resultado suma
La suma tiene
cuatro propiedades. Las propiedades son conmutativa, asociativa , distributiva y elemento neutro.
Propiedad
conmutativa: Cuando se suman dos números, el resultado es el mismo
independientemente del orden de los sumandos. Por ejemplo 4+2 = 2+4
Propiedad
asociativa: Cuando se suman tres o más números, el resultado es el
mismo independientemente del orden en que se suman los sumandos. Por ejemplo
(2+3) + 4= 2 + (3+4)
Elemento
neutro: La suma de cualquier número y cero es igual al número
original. Por ejemplo 5 + 0 = 5.
Propiedad
distributiva: La suma de dos números multiplicada por un
tercer número es igual a la suma de cada sumando multiplicado por el tercer
número. Por ejemplo 4 * (6+3) = 4*6 + 4*3
Operaciones básicas de la resta o “sustracción,
diferencia” de números naturales
-Los términos que intervienen en una resta se
llaman: a “minuendo” b
“sustraendo”, al resultado c lo llamamos
“diferencia”
La resta no es una operación
interna en el conjunto de los números naturales, porque
para que dos números naturales se puedan restar es necesario que el número
minuendo sea mayor que el número substraendo. Si eso no ocurre esa resta
no es posible en el conjunto de los números naturales porque el resultado
no sería un número natural.
La resta no tiene la propiedad conmutativa, es decir, no podemos intercambiar la posición del minuendo con la del substraendo.
La resta tampoco tiene la propiedad asociativa.
La resta no tiene la propiedad conmutativa, es decir, no podemos intercambiar la posición del minuendo con la del substraendo.
La resta tampoco tiene la propiedad asociativa.
Suma
Para sumar dos números enteros hay que tener en cuenta el signo y el valor
absoluto de cada número. Luego podemos agrupar
las reglas de la suma en dos
proposiciones.
• Para sumar dos números enteros de igual signo, sumamos los valores
absolutos y el signo del resultado coincide con
el signo que tienen los dos
números.
Ejemplos:
(+8) + (+5) = +13(-8) + (-5) =
-13
+4 + 6=10
- 4 - 6 = - 10
• Para sumar dos números enteros de distinto signo, restamos los valores
absolutos (el mayor valor absoluto menos el
menor) y el signo del resultado
coincide con el signo del número que tiene mayor
valor absoluto.
Ejemplos:
(+8) + (-5) = +3
(-8) + (+5) = -3
+ 4 - 6 = -2
- 4 + 6 =+2
• Al igual que en los números naturales el cero es el elemento neutro para
la suma de números enteros.
-9 + 0 = -9
0 - 5 = -5
(+5) + 0 = +5
Resta
Para restar dos números enteros hay que transformar la resta en una suma con la
siguiente regla:
• Para restar dos números sumamos al primer
número (minuendo) el opuesto
del segundo (sustraendo).
a - b = a + (-b)
Ejemplos:
+4 - (-3) = +4 + (+3) = +7
+4 - (+3) = +4 + (-3) = +1
-7 - (-4) = -7 + 4= -3
-7 - (+4) = -7 + (-4) = -11
Analizando los diferentes ejemplos de suma y resta de números enteros vemos
que a veces para sumar tenemos que restar y
otras veces cuando tenemos que
restar, sumamos. Es decir, todo depende de la
operación dada y de los signos de
los números
1.4 Recta Numérica.
Para construir una recta
numérica, primero se escoge un punto en la recta que
será un punto arbitrario
al que le llamaremos cero (0). Este punto es llamado
el origen de la recta
numérica. El origen separa la recta en dos partes, el lado
positivo y el lado
negativo. A la derecha del origen está el lado positivo y el
negativo está a la
izquierda. En el lado derecho van números enteros positivos
(en orden sucesivo) y en
el lado izquierdo se escriben los números enteros
negativos (en orden
sucesivo), estos se marcan en unidades equidistantes.
RECTA NUMERICA
Es importante
recordar que para cualesquiera dos números reales diferentes a los que
llamaremos a y b, siempre uno es mayor que el otro.
Si a - b es
positivo, entonces
Si b - a es
positivo, entonces
USO DE LOS SIGNOS DE AGRUPACIÓN Y
OPERACIONES EN LOS ENTEROS
Dentro de los
signos de agrupación tenemos:
( ) Paréntesis
[ ] Corchetes
signos de agrupación
{ } Llaves
Se usan para
agrupar operaciones, facilitan el orden al operar, cuando tienes una operación,
ejemplo:
Algunas veces se
hace necesario realizar operaciones de suma y resta con más de dos números
enteros, por ejemplo:
La diferencia
entre un signo de agrupación y otro es sólo que se usan en este orden: el
más interno: paréntesis, luego viene el corchete, y el más externo es la llave.
Un signo delante de un paréntesis o de un corchete, o de una
llave, indica
que se tomará el opuesto de todo lo que hay dentro del signo
de agrupación.
Deberán, entonces, realizarse las operaciones que están
dentro de cada signo
de agrupación y luego cambiarse el signo en este caso. Si el
paréntesis, el
corchete o la llave están precedidos por un signo +, no se
cambia el signo
de lo que está dentro de los signos de agrupación. Para
realizar la operación
anterior, se comienza por operar con lo que hay dentro de
los signos de
agrupación más internos:
Los paréntesis.
Así la expresión:
Se transforma en:
Ahora se calcula lo que hay dentro de los corchetes:
y se escribe:
Resolviendo las operaciones dentro de las llaves, se obtiene
y así la expresión original es igual a:
Ejemplo N° 2
Ejemplo N° 3
Ejemplo N° 4
4-2 x { 3 x [ 5-2 x (5-6) – 7 ] + 10 } + 17 =
4-2 x {3 x [5- 2x(-1) -7 ] + 10 } + 17 =
= 4-2 x {3 x [ 5+2-7
] + 10 } + 17 = 4-2 x { 3 0+10 } + 17=
= 4-2 x { 0+10 } + 17 = 4-2 x 10+17 = 4 -
20+17 = 21- 20 = 1
Ejemplo N° 5
Operaciones
aritméticas combinadas
Primero operamos con los productos y números mixtos de los
paréntesis.
Operamos en el primer paréntesis, quitamos el segundo,
simplificamos en el
tercero y operamos en el último.
Realizamos el producto y lo simplificamos.
Realizamos las operaciones del paréntesis.
Hacemos las operaciones del numerador, dividimos y
simplificamos el resultado.
Nota: Resuelve las multiplicaciones y divisiones antes de
las sumas y restas. Resuelve
las multiplicaciones y divisiones “en el mismo nivel,” de
izquierda a derecha. Resuelve las sumas y restas “en el mismo nivel,” de
izquierda a derecha. Los paréntesis ( ) cambian el orden. Resuelve primero lo
que está adentro de los paréntesis.
TALLER N. 1
En los ejercicios siguientes, simplifique. Asegúrese de
suprimir todos los
paréntesis y simplificar todas las fracciones:
- 2 ∗[3 − 2 ∗ (4 − 8)]
2. 5 − 4 ∗ (12 − 8)+ 9
3. − 2 ∗ (3 − 4)+ 3∗
(7 − 5)
4. − 4 ∗ [3 ∗
(− 6 +13)− 2 ∗ (5 −
9)−116]
5. 3∗[6 − 2 ∗
(4 − 7)+ 2]− 5
6. [81+ (− 54)]*[(−14)+19]
7. [(− 43)− (− 28)]*{(−18)−
(−16)}
8. [8 + (− 5)]*[(−1)+ 9]
9. [(−14)+15]*[(−16)+ (− 27)]
10. [(−1)+11− (−{5 + 3 −11}−10)∗{− (−15 + 4 + 21)}]*[(− 6)+
(− 7)]
2.1 MULTIPLICACIÓN
Operaciones básicas de la
multiplicación o “producto”
- Propiedad conmutativa: El orden de los factores no varía el producto.
Vamos a ver un ejemplo de la propiedad conmutativa.
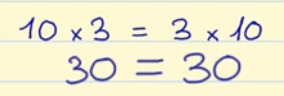
El resultado de multiplicar 10 x 3 será igual que al multiplicar 3 x 10. Aunque cambiemos el orden de los factores el resultado seguirá siendo 30.
- Propiedad asociativa: El modo de agrupar los factores no varía el resultado de la multiplicación.
Pongamos un ejemplo de la propiedad asociativa de la multiplicación.
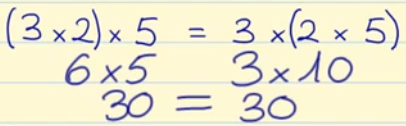
En este caso, como mostramos en la imagen, nos dará el mismo resultado si multiplicamos 3 x 2 y después lo multiplicamos por 5, que si multiplicamos 2 x 5 y después lo multiplicamos por 3.
- Elemento neutro: El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.
En el ejemplo que os mostramos en la imagen, vemos que si multiplicamos 5 o 7 por la unidad, nos da como resultado 5 o 7. Por lo tanto cualquier número que multipliquemos por 1, nos dará como resultado el mismo número.
- Propiedad distributiva: La multiplicación de un número por una suma es igual a la suma de las multiplicaciones de dicho número por cada uno de los sumandos.
Pongamos un ejemplo: 2 x (3 + 5)
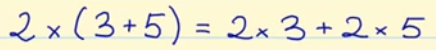
Según la propiedad distributiva 2 x (3 + 5) será igual a 2 x 3 + 2 x 5
Comprobemos si esto es cierto.
2 x (3 + 5) = 2 x 8 = 16
2 x 3 + 2 x 5 = 6 + 10 = 16
Ambas nos dan como resultado 16, por lo que queda demostrada la propiedad distributiva de la multiplicación.
Utilizando símbolos de agrupación para realizar multiplicaciones:
Ejemplo:
[(3× (−5))× 2]= [(−15) × 2]= −30
[(4 × 3)× ((−3) × 7)]= − [12 × (−21)] = = − [− 252]= 252
*En este caso el signo (-) que esta antepuesto al corchete significa que se está multiplicando por (-1) por tal razón (-1) por el valor dentro del corchete (-252) es igual a 252. Se aplicó la ley que dice que un número negativo multiplicado por otro negativo el resultado es un número positivo.
2.2 DIVISION
Operaciones básicas de la división o “cociente”
La división es la operación inversa a la multiplicación. Consiste en averiguar cuántas veces el divisor está contenido en el dividendo.
División exacta:
Es aquella en la que el resto vale cero.
La propiedad fundamental es que el dividendo es siempre igual al resultado de multiplicar el divisor por el cociente.
Dividendo = divisor x cociente
45 : 5 = 9 entonces 45 = 5 x 9
División entera:
Es la que tiene un resto distinto de cero.
En estas divisiones el Dividendo ha de ser igual al divisor por el cociente más el resto.
Dividendo = divisor x cociente + resto
48 : 5 = 9 y sobran tres de resto. Entonces 48 = 5 x 9 + 3
Esta operación que acabamos de indicar es a lo que se le llama hacer la prueba de la división.
Muy importante:
Hay que tener en cuenta siempre que el resto debe ser necesariamente menor que el divisor.
También es de gran importancia recordar que nunca se puede dividir por cero. Si dividir es hacer un reparto, no puedo dividir (repartir) si no hay nadie a quien repartirle (divisor cero).
Taller N2
1. Realizar las siguientes operaciones..
1. ( + 4 ) + ( - 10)
2. ( - 4 ) + ( - 7 )
3. ( - 5 ) + ( + 15 )
4. ( 2 + 5 ) + (- 7)
5. [ ( - 5 ) + ( - 10 ) ] + (+ 4)
6. [ ( + 4 ) + ( - 5 ) ] + (- 7)
7. ( + 4 ) + ( - 10 )
8. ( - 5 ) + ( + 15 )
9. [ ( - 5 ) + ( - 10 ) ] + ( + 4 )
10. [ ( + 4 ) + ( - 5 ) ] + ( - 7 ) ( + 4) + ( - 10 )
2. Hallar el resultado para cada caso:
1. [(3 − 7)+15]
2. [(8 − 9)+ (10 + 2)]+ [(6 + 5)− 2]
3. [(− 2 + 4)+ (5 + 7)]− {[(7 − 4)+ 5]−10}
4. {{[(− 3 − 9)+ 7]−10}+ 7}− [(3 + 2)− (7 −10)]
5. [8 + (− 5)]* [(− 1)+ 9]
6. [(− 1)+ 11]* [(− 6)+ (− 7)]
7. [(− 3)− (− 8)]* [(− 8)− (− 6)]
8. [(− 4)+ 7]* [− (− 6)* (− 3)]
9. [(− 43)− (− 28)]*{(−18)− (−16)}
2.3 MÍNIMO COMÚN MÚLTIPLO
El mínimo común múltiplo (M.C.M. o mcm) de varios números es el menor de sus
múltiplos comunes.
NOTA:
El M.C.M. también llamado m.c.d. (mínimo común denominador), pues esutilizado para sumar fracciones heterogéneas o fracciones con diferente denominador, tema que se aclarará después.
Ejemplo N. 1
Encuentra el mínimo común múltiplo de 3 y 5:
Los múltiplos de 3: 3, 6, 9, 15, 18, 21, 24, 27, 30, ...,
Los múltiplos de 5: 5, 10, 15, 20, 25, 30, 35, 40, ...,
Respuesta: 15
Como puedes ver en esta línea de números, el primer múltiplo que coincide es el 15.
Ejemplo 2: Calcula el mínimo común múltiplo de 4, 6 y 8
Los múltiplos de 4 son: 4, 8, 12, 16, 20, 24, 28, 32, 36,...
Los múltiplos de 6 son: 6, 12, 18, 24, 30, 36,...
Los múltiplos de 8 son: 8, 16, 24, 32, 40,....
Respuesta: 24
Para calcular el mínimo común múltiplo:
Se factoriza los números tomamos todos los factores (comunes y no comunes) elevados a los mayores exponentes.El es el producto de los factores anteriores
Ejemplo N. 3
Los factores son: y elevados a los mayores exponentes (dentro de un recuadro)serían:
Multiplicando los factores anteriores se obtiene el
EJERCICIO N. 1
Hallar el mínimo común múltiplo de:
1. 48 y 16
2. 52 y 64
3. 26 y 42
4. 38 y 46
5. 36,48 y 12
2.4 MAXIMO COMÚN DIVISOR
El Máximo Común Divisor (M.C.D. o MCD) de varios números es el mayor de sus divisores comunes.
Para calcularlo: Factorizamos los números tomamos todos los factores comunes elevados a los menores exponentes
El M.C.D. es el producto de los factores anteriores
Factores comunes (a todos los números): 2, y elevado al menor exponente (dentro
de un recuadro) sería: 22
EJERCICIO N.2
Hallar el máximo común divisor de:
1. 48 y 16
2. 54 y 45
TALLER N. 3
1. Hallar el mínimo común múltiplo de:
1. 48 y 16
2. 52 y 64
3. 26 y 42
4. 38 y 46
5. 36,48 y 12
. Por tanto;
3. 1000 y 1500
4. 84 y 72
5. 860,240 y 168
2. Hallar el máximo común divisor de:
1. 48 y 16
2. 54 y 45
3. 1000 y 1500
4. 84 y 72
5. 860,240 y 168
3. Completa los espacios que están vacíos en las series siguientes:
a) 3, 6, 9, 12, _____, 18, 21, _____, _____
b) ___, 10, 15, 20, 25, ____, 35, _____
c) 7, 14, 21, ____, 35, _____, _____
d) 12, 24, _____, 48, _____, ______
e) _____, 38, 57, ______, ______
4. Escribe los diez primeros múltiplos de 5:____________________________
5. Escribe los primeros diez múltiplos de 3:____________________________
Escribe los elementos comunes de estos dos conjuntos:_________________
¿Cuál es el menor? _______
Ese número es el MÍNIMO COMÚN MÚLTIPLO ó MCM de los punto 2 y 3.
6. Siguiendo los pasos del ejercicio anterior, encuentra el mínimo común múltiplo
de 10 y 12
Múltiplos de 10:_________________________________________________
Múltiplos de 12:_________________________________________________
MCM (10,12) = _________________________________________________
3 NÚMEROS FRACCIONARIOS
Los números fraccionarios se simbolizan con la letra (Q). Se clasifican en
Racionales (Q) y números Irracionales (Q`). Se pueden representar en la recta
numérica al igual que otros números reales.
Los números fraccionarios tienen tres partes a saber:
Un fraccionario puede ser negativo o positivo, lo que indica el signo es que
la operación está realizando frente a otras fracciones y si se ubica en la recta
numérica el sentido en el cual se localiza.


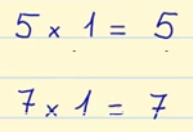



No hay comentarios:
Publicar un comentario