Ecuaciones lineales

                                                                               

Ecuaciones Lineales

Sabemos que una ecuación lineal o de primer grado es aquella que involucra solamente sumas y restas de variables elevadas a la primera potencia (elevadas a  uno, que no se escribe). Son llamadas lineales por que se pueden representar como rectas en el sistema cartesiano.

Se pueden presentar tres tipos de ecuaciones lineales:

a) ecuaciones lineales propiamente tales

En este tipo de ecuación el denominador de todas las expresiones algebraicas es igual a 1 (no se presentan como fracción, aunque el resultado sí puede serlo). 

Para proceder a la resolución se debe:

Eliminar paréntesis.

Dejar todos los términos que contengan a "x" en un miembro y los números en el otro.

Luego despejar "x" reduciendo términos semejantes.

Ejemplo:

4x – 2(6x – 5) = 3x + 12(2x + 16)

4x – 12x + 10 = 3x + 24x + 192

4x – 12x – 3x – 24x = 192 – 10

–35x = 182

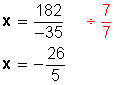
b) ecuaciones fraccionarias

En este tipo de ecuación lineal el denominador de a lo menos una de las expresiones algebraicas es diferente de 1 (es una fracción). 

Para proceder a la resolución se debe:

Llevar a ecuación lineal (eliminar la fracción) multiplicando la ecuación por el mínimo común múltiplo de los denominadores (m.c.m.)

Ejemplo:

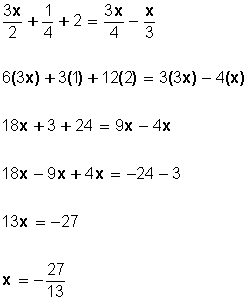
m.c.m. de 2, 4 y 3 = 12

c) ecuaciones literales

Pueden ser lineales o fraccionarias. Si son fraccionarias, se llevan al tipo lineal, pero en el paso de reducir términos semejantes se factoriza por "x" para despejarla.

Ejemplo:

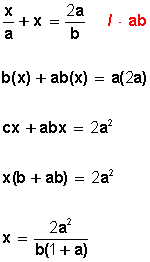
Las ecuaciones lineales se encuentran entre los tipos más simples de ecuaciones. Tienen unas pocas variables simples que se combinan para formar una respuesta. En la mayoría de los casos, simplemente deberás despejar la variable x o y. Como mucho, deberás resolver ambas. Las ecuaciones lineales son diferentes a las radicales porque no tienen radicales, lo cual cambia el modo en que son resueltas. Resolver ecuaciones lineales pueden ser relativamente fácil de aprender si simplemente recuerdas unos pocos pasos fáciles.

1  

Remueve cualquier paréntesis en tu ecuación lineal primero. Haz esto multiplicando la variable más cercana a la izquierda del paréntesis por cada uno de los valores dentro del mismo.

2

Combina todos los términos semejantes en tu ecuación. En la ecuación del ejemplo, esto significaría sumar 7 y -27.

3

Aísla la variable a resolver realizando el mismo proceso en ambos lados. Si tu ecuación original requiere que añadas un número a la variable, sustrae ese número de ambos lados. Si originalmente multiplicas un número por la variable, divide ambos lados por ese mismo número y así sucesivamente.

4

Ecuaciones de primer grado

Ecuaciones de primer grado, ejemplos y ejercicios resueltos de ecuaciones con paréntesis y denominadores.

Concepto

Para que exista una ecuación tiene que haber algo igual a algo. Una ecuación es de primer grado cuando la x (la variable) está elevada a uno.

Pasos para resolver una ecuación de primer grado

Si hay denominadores, los reducimos a común denominador (calculando el m.c.m ) y suprimimos los denominadores.

Quitamos los paréntesis aplicando la regla de los signos.

Al final tendremos a ambos lados del =, sólo sumas y restas, unos términos llevaran x y otros no.

Transposición de términos: Pasamos todos los términos con x a un lado de la ecuación, los números al otro lado.

Agrupamos los términos semejantes y al final despejamos la x obteniendo la solución.

Comprobamos la solución sustituyendo el valor de la x obtenida en la ecuación. Nos tiene que dar el mismo resultado a ambos lados de la ecuación.

Soluciones de una ecuación de primer grado. Ejemplos

Un número real: es cuando normalmente decimos que nos da solución.

x + 3 = 5 x + 11    =>   x - 5 x = 11 - 3   =>   - 4 x = 8   =>   x = 8 / - 4   => x = - 2

Todo número real: no importa el valor de x, nos da    =>  0 x = 0

13 - 3 x - 9 = 8 x + 4 - 11 x    =>   - 3 x - 8 x + 11 x = 4 + 9 - 13    =>   0 = 0

Incompatible: se anulan las x y nos da    =>  0 x = número. No tiene solución.

6 + 5 x + 2 = 4 x - 2 + x    =>   5 x - 4 x - x = - 2 - 6 - 2    =>   0 x = - 10

Ejercicios resueltos

Resolver ecuaciones de primer grado

•